Central tendency and dispersion
There are multiple measures of central tendency (these are all averages so you must be careful when you say that word to explain which type you mean!):
Mean: the sum of all points divided by the total number of points; susceptible to outliers
Median: the middlemost value; less susceptible to outliers and best used when the data is skewed
Mode: most frequent score
- Multimodal or bimodal: when two or more values are the most frequent score
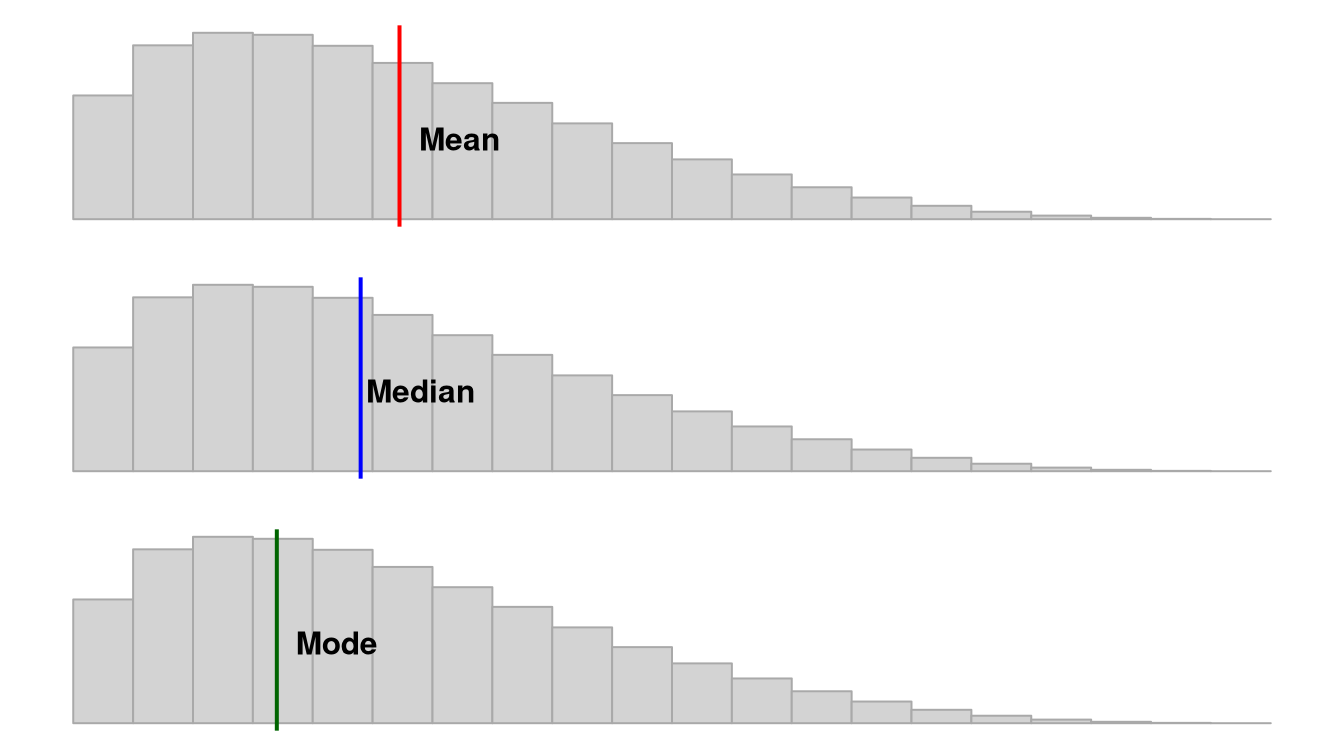
Note that depending on the shape of the distribution, the mean, median, and mode may not be the same value. If we have a normal distribution then they will be the exact same! However, if we have a positively skewed distribution, the mean and median will be pulled towards the positively skewed data, as shown in this figure by Peter Prevos.
There are also multiple measures of dispersion that describe the spread of our data:
Range: the difference between the maximum and minimum value (e.g., if the minimum score is 17 and the maximum is 49, then the range is 32)
Quartile: when a dataset is divided into four equal parts, the first quartile (Q1) is at the 25th percentile, the second quartile (Q2) is at the 50th percentile, and the third quartile (Q3) is at the 75th percentile.
- Interquartile range: the middle 50% (Q1 to Q3)
Variance: the sum of the squared deviations from the mean. This means first (a) calculating the mean, (b) subtracting each score from the mean (aka deviations from the mean), (c) squaring each of those deviations values, and (d) summing all those squared deviations. This is represented by the equation \(\frac{\sum (X-\mu)^2}{N}\)
Standard deviation: is the square of the variance. This is represented by the equation \(\sqrt{\frac{\sum (X-\mu)^2}{N}}\) however that equation is only used if we are examining the whole population. If we only have a sample, we replace the denominator
NwithN-1.
We also have two main measures of shape that describe the shape of the distribution of our data:
Skew: in a non-normal distribution, it is when one tail of the distribution is longer than another. Present in asymmetric distributions
Negative skew: when the tail points to the negative end of the spectrum; in other words, most of the values are on the right side of the distribution
Positive skew: when the tail points to the positive end of the spectrum; in other words, most of the values are on the left side of the distribution
Kurtosis: the weight of the tails relative to a normal distribution. There are some fancy terms related to kurtosis that you may hear about, but honestly I don’t hear them used very frequently by researchers.
- Leptokurtic: light tails; values are more concentrated around the mean
- Platykurtic: heavy tails; values are less concentrated around the mean
There are other terms we use to describe data:
Frequency distribution: overview of the times each value occurs in a dataset; often portrayed visually like with a histogram
Histogram: a visual depiction of the frequency distribution using bars to depict a range of the distribution
Normal distribution: a special distribution in which the data are symmetrical on both sides of the mean; under a normal distribution, the mean is also equal to the median